3.9 – Practice Problem 1

A waste stream containing 5.15 wt% chromium enters a waste water treatment process. The treatment unit has a maximum intake capacity of 4500 kg wastewater/h. The treatment unit extracts 95% of the chromium in the feed. The residual liquid leaving the treatment unit is sent to a waste lagoon. If there is an excess of waste water (greater than the 4500 kg/h capacity), the excess waste water bypasses the treatment unit and combines with the residual liquid stream that goes to the waste lagoon. Suppose 6000 kg wastewater/h enters the process.

1. Draw and label a flowchart of the entire process.
2. Perform a degree of analysis on each unit operation and determine which unit should be solved first.
3. Solve and label the entire process.

Answer

a) Draw and label a flowchart of the entire process.

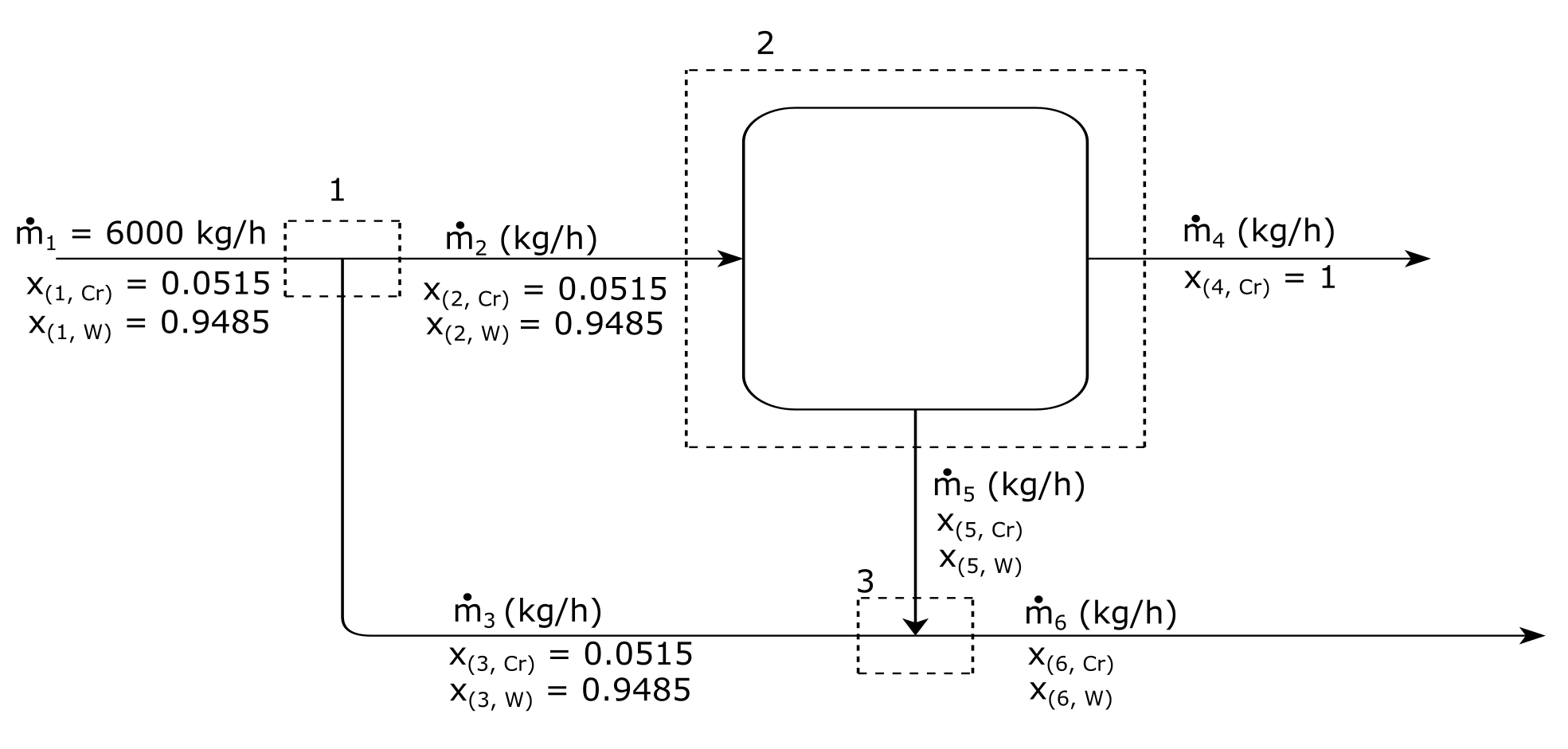
b) Perform a degree of freedom analysis on each unit operation and determine which unit should be solved first.

Lets first write out all the equations for each of the unit ops.

1. Since we know the treatment unit has a maximum capacity of 4500 kg/h, and \(\dot{m}_1 = 6000 kg/h\), we can solve for \(\dot{m}_3\). We also know that a splitter has the same composition for all of the streams.

   \[\dot{m}_2 = 4500 \space \frac{kg}{h}\]
   \[\dot{m}_3 = \dot{m}_1 - \dot{m}_2\]
   \[\]

2. We have a relating equation to help us solve this unit op.

   \[\dot{m}_2 = \dot{m}_4 + \dot{m}_5\]
   \[\dot{m}_2 x_{(2, \space Cr)} = \dot{m}_4 x_{(4, \space Cr)} + \dot{m}_5 x_{(5, \space Cr)}\]
   \[\dot{m}_4 = \big(0.95 \big) \dot{m}_2 x_{(2, \space Cr)}\]
   \[x_{(5, \space w)} = 1 - x_{(5, \space Cr)}\]
   \[\]
3. \[\dot{m}_3 + \dot{m}_5 = \dot{m}_6\]
   \[\dot{m}_3 x_{(3, \space Cr)} + \dot{m}_5 x_{(5, \space Cr)} = \dot{m}_6 x_{(6, \space Cr)}\]
   \[x_{(6, \space w)} = 1 - x_{(6, \space Cr)}\]

Now lets perform the degree of freedom analysis on each unit.

1. \[DOF = 2 - 2 = 0\]
   \[\]
2. \[DOF = 5 - 4 = 1\]
   \[\]
3. \[DOF = 5 - 3 = 2\]

With this degree of freedom analysis, we can observe that the online unit op that is solvable right away is the splitter.

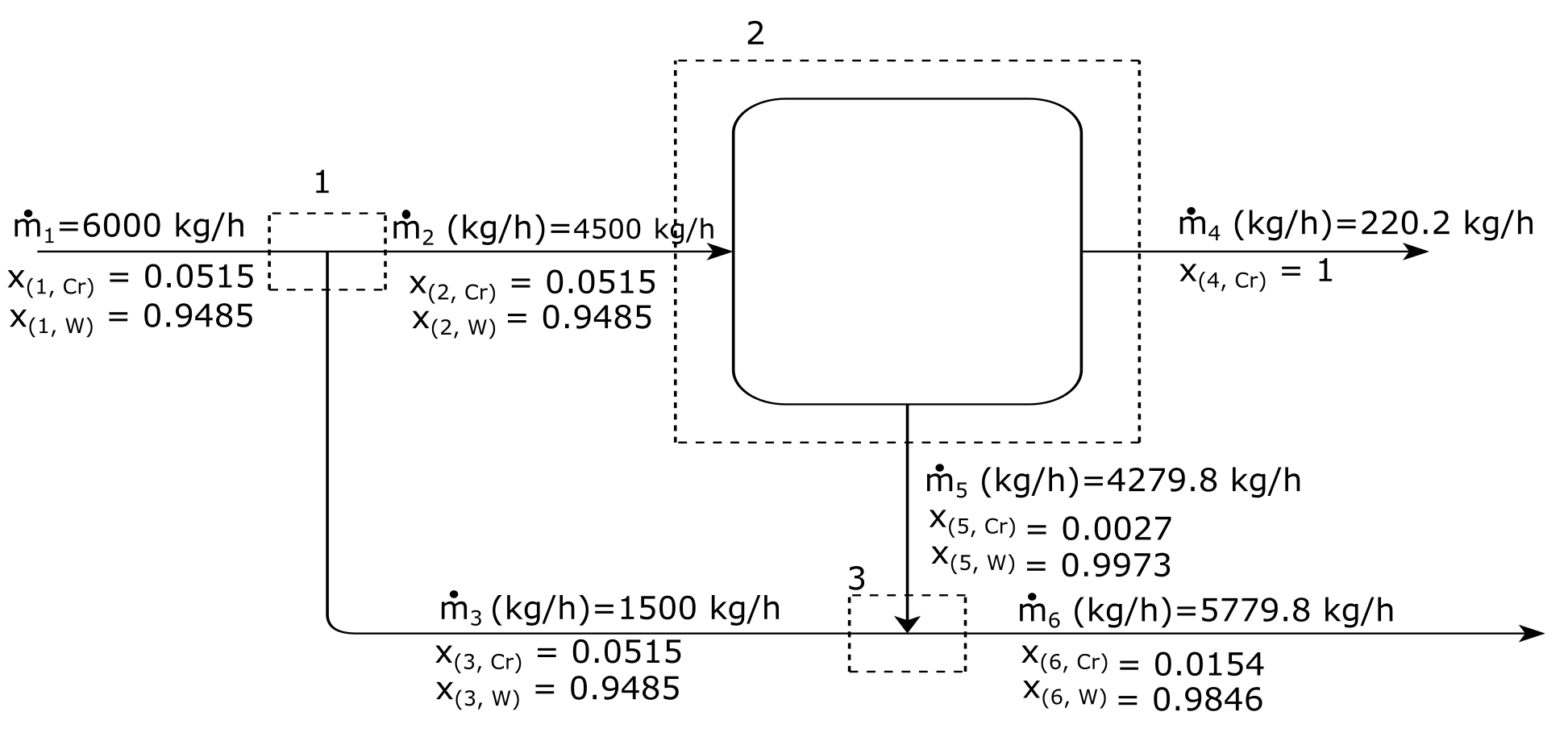
c) Solve the entire process.

First let’s solve for the splitter.

\[\dot{m}_1 = 6000 \space \frac{kg}{h}\]

\[\dot{m}_2 = 4500 \space \frac{kg}{h}\]

\[\dot{m}_3 = \dot{m}_1 - \dot{m}_2 = 1500 \space \frac{kg}{h}\]

Now that we have the mass flowrate for \(\dot{m}_2\) we can solve the separator.

\[\dot{m}_4 = \big(0.95 \big) \dot{m}_2 x_{(2, \space Cr)} = \big(0.95 \big) \cdot \big(4500 \big) \cdot \big(0.0515 \big)\]

\[\dot{m}_4 = 220.2 \space \frac{kg}{h}\]

\[\dot{m}_5 = \dot{m}_6 - \dot{m}_3 = 4500 - 220.2 = 4279.8 \space \frac{kg}{h}\]

\[x_{(5, \space Cr)} = \frac{\dot{m}_4 x_{(4, \space Cr)} - \dot{m}_2 x_{(2, \space Cr)}}{ \dot{m}_5} = \frac{\big(220.2 \big) \big(1\big) + \big(4500\big)\big(0.0515\big)}{4279.8} = 0.0027\]

\[x_{(5, \space w)} = 1 - x_{(5, \space Cr)} = 1 - 0.0027 = 0.9973\]

We can solve for the mixer unit op.

\[\dot{m}_6 = \dot{m}_3 + \dot{m}_5 = 1500 + 4279 = 5779.8 \space \frac{kg}{h}\]

\[x_{(6, \space Cr)} = \frac{\dot{m}_3 x_{(3, \space Cr)} + \dot{m}_5 x_{(5, \space Cr)}}{ \dot{m}_6} = \frac{\big(1500 \big) \big(0.0515\big) + \big(4279.8\big)\big(0.0027\big)}{5779.8} = 0.0154\]

\[x_{(6, \space w)} = 1 - x_{(6, \space Cr)} = 1 - 0.0154 = 0.9846\]

Finally, we can complete the flowchart.